请注意,本文编写于 182 天前,最后修改于 182 天前,其中某些信息可能已经过时。
目录
引言
在地理信息系统(GIS)、导航和位置服务等应用中,计算地球表面两点之间的距离是一个常见需求。本文将介绍如何使用C#和Gaversin公式来准确计算这个距离。
Gaversin公式简介
Gaversin公式(也称为Haversine公式)是计算球面上两点之间大圆距离的一种方法。在地球这个近似球体上,它可以给出两点间的最短距离。与简单的直线距离相比,Gaversin公式考虑了地球的曲率,因此在计算长距离时更为准确。
C#实现
让我们看看如何用C#实现Gaversin公式:
C#public class GeoCalculator
{
private const double EarthRadiusKm = 6371.0;
public double CalculateDistance(double lat1, double lon1, double lat2, double lon2)
{
var dLat = DegreesToRadians(lat2 - lat1);
var dLon = DegreesToRadians(lon2 - lon1);
var a = Math.Sin(dLat / 2) * Math.Sin(dLat / 2) +
Math.Cos(DegreesToRadians(lat1)) * Math.Cos(DegreesToRadians(lat2)) *
Math.Sin(dLon / 2) * Math.Sin(dLon / 2);
var c = 2 * Math.Atan2(Math.Sqrt(a), Math.Sqrt(1 - a));
return EarthRadiusKm * c;
}
private static double DegreesToRadians(double degrees)
{
return degrees * Math.PI / 180;
}
}
代码解释
EarthRadiusKm: 地球平均半径(单位:公里)。CalculateDistance: 主要方法,接收两点的经纬度,返回距离。DegreesToRadians: 辅助方法,将角度转换为弧度。- 在
CalculateDistance方法中:- 计算纬度和经度的差值
- 使用Gaversin公式计算距离
- 返回结果(单位:公里)
使用示例
下面是如何使用这个类的示例:
C#class Program
{
static void Main(string[] args)
{
var calculator = new GeoCalculator();
// 示例1: 北京到上海
double beijingLat = 39.9042, beijingLon = 116.4074;
double shanghaiLat = 31.2304, shanghaiLon = 121.4737;
double distance = calculator.CalculateDistance(beijingLat, beijingLon, shanghaiLat, shanghaiLon);
Console.WriteLine($"北京到上海的距离: {distance:F2} 公里");
// 示例2: 纽约到伦敦
double newYorkLat = 40.7128, newYorkLon = -74.0060;
double londonLat = 51.5074, londonLon = -0.1278;
distance = calculator.CalculateDistance(newYorkLat, newYorkLon, londonLat, londonLon);
Console.WriteLine($"纽约到伦敦的距离: {distance:F2} 公里");
// 示例3: 悉尼到东京
double sydneyLat = -33.8688, sydneyLon = 151.2093;
double tokyoLat = 35.6762, tokyoLon = 139.6503;
distance = calculator.CalculateDistance(sydneyLat, sydneyLon, tokyoLat, tokyoLon);
Console.WriteLine($"悉尼到东京的距离: {distance:F2} 公里");
}
}
输出结果
运行上述代码,你将得到类似以下的输出:
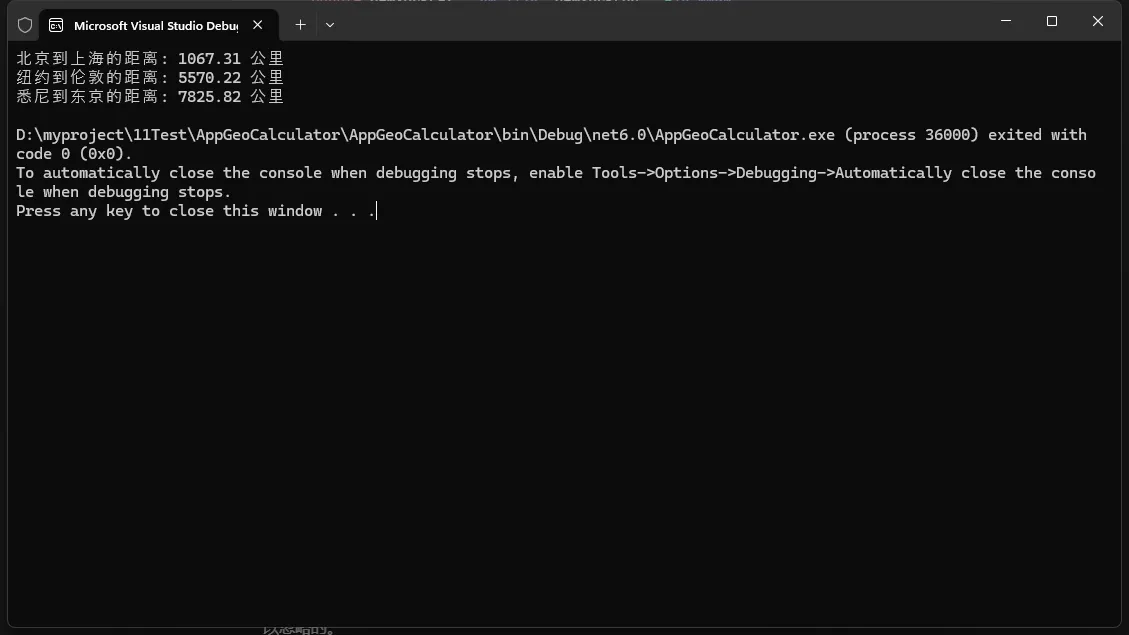
注意事项
- 精度: Gaversin公式假设地球是完美的球体,实际上地球略微扁平。对于大多数应用来说,这个误差是可以忽略的。
- 单位: 本实现使用公里作为单位。如果需要其他单位(如英里),只需在返回结果时进行单位转换。
- 性能: 对于需要频繁计算大量距离的应用,可以考虑使用查找表或其他优化方法来提高性能。
结论
Gaversin公式提供了一种简单而相对准确的方法来计算地球表面两点之间的距离。通过C#实现,我们可以轻松地将这个功能集成到各种应用中,如旅行规划器、物流系统或位置基础服务等。
本文作者:rick
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
目录