作为一名C#开发者,你是否遇到过这样的困扰:Timer没有及时释放导致内存泄漏?异步任务无法优雅取消?事件订阅忘记解除导致对象无法回收?这些看似简单的资源管理问题,往往成为项目中的"定时炸弹"。
今天给大家分享一个强大的资源管理模式——ActionDisposable,它能够统一管理各种资源,让你的代码更加健壮,彻底告别资源管理的烦恼。这不是什么高深的理论,而是一个立即可用的实战技巧!
🔥 痛点分析:资源管理的常见陷阱
在日常开发中,我们经常需要管理各种资源:
传统做法的问题:
- Timer对象忘记Dispose,导致后台线程持续运行
- 事件订阅没有及时解除,形成强引用链
- 异步任务的CancellationTokenSource管理混乱
- 多个资源分散管理,容易遗漏
C#// ❌ 传统的问题代码
public class BadExample : IDisposable
{
private Timer _timer;
private CancellationTokenSource _cts;
public BadExample()
{
_timer = new Timer(Callback, null, 1000, 1000);
_cts = new CancellationTokenSource();
SomeEvent += OnSomeEvent; // 容易忘记取消订阅
}
// 经常忘记实现或实现不完整
public void Dispose()
{
_timer?.Dispose(); // 如果忘记这行呢?
_cts?.Cancel(); // 如果这里抛异常呢?
// SomeEvent -= OnSomeEvent; // 经常忘记这行
}
}
你是否在开发桌面应用自动化测试时,面对复杂的界面元素定位而头疼?是否在处理不同控件交互时,总是找不到合适的方法?作为一名资深的C#开发者,我发现许多同行都在UI Automation的学习路上踩过这些坑:不理解UI自动化树结构、找不准控件元素、搞不清楚控件模式的使用场景。
今天这篇文章,我将带你深入理解UI Automation的四大核心概念,通过实战代码和真实场景,让你彻底掌握这些技术要点,从此告别"盲人摸象"式的开发模式!
💡 核心概念深度解析
🌳 UI Automation Tree:桌面应用的"DOM树"
什么是UI自动化树?
UI Automation Tree就像网页的DOM树一样,是Windows桌面应用程序界面元素的层次化表示。每个窗口、按钮、文本框都是这棵树上的一个节点,通过父子关系组织起来。
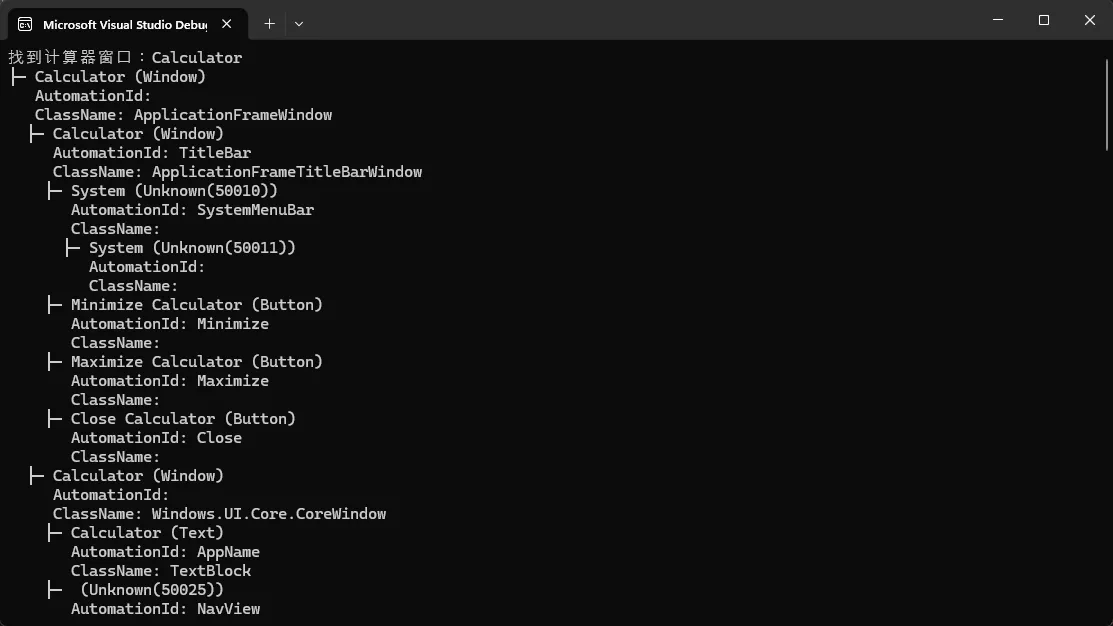
实战场景:定位计算器中的按钮
C#using UIAutomationClient;
namespace AppAutomationTreeExample
{
internal class Program
{
static void Main(string[] args)
{
Console.OutputEncoding = System.Text.Encoding.UTF8;
CUIAutomation8 automation = new CUIAutomation8();
var desktop = automation.GetRootElement();
var windowCondition = automation.CreateAndConditionFromArray(new[]
{
automation.CreatePropertyCondition(
UIA_PropertyIds.UIA_NamePropertyId, "Calculator"),
automation.CreatePropertyCondition(
UIA_PropertyIds.UIA_ControlTypePropertyId,
UIA_ControlTypeIds.UIA_WindowControlTypeId)
});
var calcWindow = desktop.FindFirst(TreeScope.TreeScope_Children, windowCondition);
if (calcWindow != null)
{
Console.WriteLine($"找到计算器窗口:{calcWindow.CurrentName}");
// 🎯 分析整个UI树结构
AnalyzeUITree(calcWindow, automation, 0, 5); // 最多5层深度
}
}
// 🔥 递归分析UI树结构
static void AnalyzeUITree(IUIAutomationElement element, CUIAutomation8 automation, int level, int maxLevel)
{
if (level > maxLevel) return;
string indent = new string(' ', level * 2);
string controlType = GetControlTypeName(element.CurrentControlType);
Console.WriteLine($"{indent}├─ {element.CurrentName} ({controlType})");
Console.WriteLine($"{indent} AutomationId: {element.CurrentAutomationId}");
Console.WriteLine($"{indent} ClassName: {element.CurrentClassName}");
// 查找所有子元素
var children = element.FindAll(TreeScope.TreeScope_Children,
automation.CreateTrueCondition());
for (int i = 0; i < children.Length; i++)
{
AnalyzeUITree(children.GetElement(i), automation, level + 1, maxLevel);
}
}
// 获取控件类型名称
static string GetControlTypeName(int controlTypeId)
{
var controlTypes = new Dictionary<int, string>
{
{ UIA_ControlTypeIds.UIA_ButtonControlTypeId, "Button" },
{ UIA_ControlTypeIds.UIA_WindowControlTypeId, "Window" },
{ UIA_ControlTypeIds.UIA_PaneControlTypeId, "Pane" },
{ UIA_ControlTypeIds.UIA_GroupControlTypeId, "Group" },
{ UIA_ControlTypeIds.UIA_TextControlTypeId, "Text" },
{ UIA_ControlTypeIds.UIA_EditControlTypeId, "Edit" }
};
return controlTypes.ContainsKey(controlTypeId) ? controlTypes[controlTypeId] : $"Unknown({controlTypeId})";
}
}
}
作为一名在工业软件领域摸爬滚打多年的老程序员,我发现很多开发者对观察者模式的理解往往停留在理论层面。最近在为某大型制造企业开发设备监控系统时,我深刻体会到了观察者模式在实际项目中的强大威力。想象一下:当生产线上的温度传感器数值异常时,监控大屏、报警系统、数据库记录模块都能第一时间收到通知并作出响应,这种松耦合的设计让系统既稳定又易于扩展。
今天就来分享一套完整的工业监控系统实现方案,帮你彻底掌握观察者模式的实战应用。
🤔 为什么传统的监控系统难以维护?
紧耦合带来的痛点
在没有使用观察者模式之前,我们通常会这样写代码:
C#// ❌ 传统的紧耦合写法
public class Sensor
{
private MonitorPanel panel;
private AlarmSystem alarmSystem;
private DatabaseLogger logger;
public void UpdateValue(double newValue)
{
this.value = newValue;
// 直接调用各个模块
panel.UpdateDisplay(this.name, newValue);
if(newValue > maxValue)
alarmSystem.TriggerAlarm(this.name, newValue);
logger.LogData(this.name, newValue);
}
}
这种写法存在明显问题:
- 维护噩梦:每次新增监控模块都要修改Sensor类
- 测试困难:无法独立测试各个组件
- 扩展性差:系统规模越大,耦合越严重
🎯 观察者模式:解耦的艺术
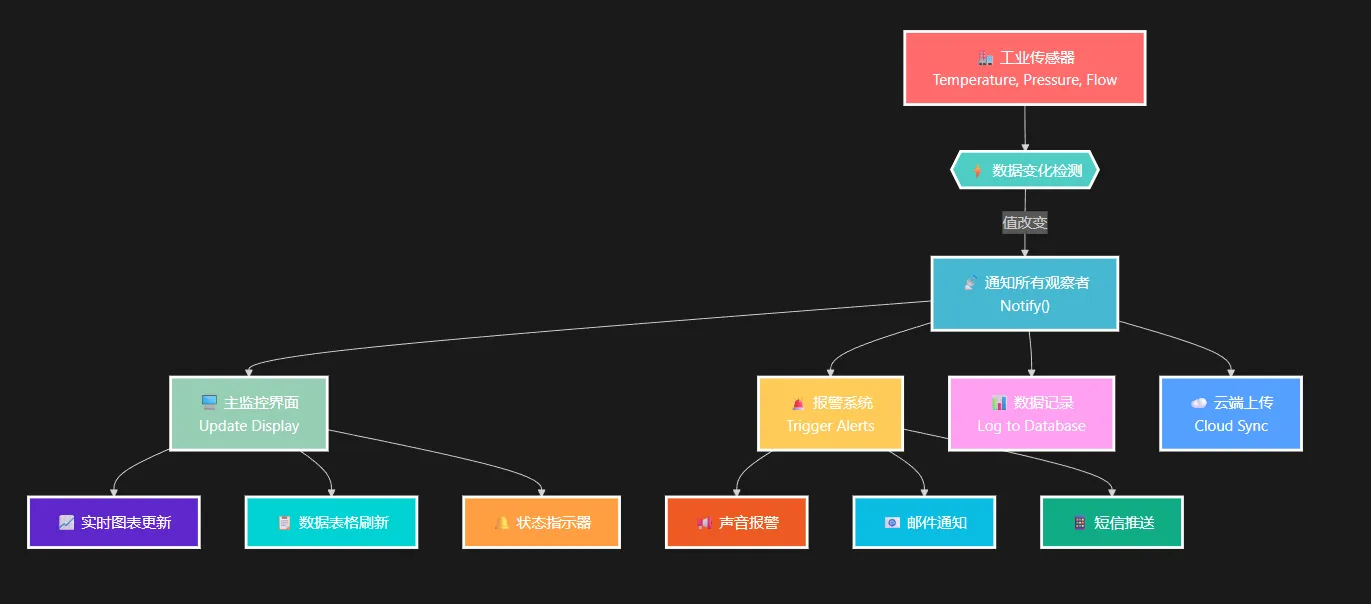
核心设计思想
观察者模式通过定义一对多的依赖关系,让多个观察者对象同时监听某一个主题对象,当主题状态发生变化时,所有观察者都会收到通知。
你是否遇到过这样的开发场景:需要在某个应用程序关闭后自动执行清理操作?或者开发自动化测试工具时,需要等待被测应用退出后生成测试报告?又或者在开发插件管理器时,需要在主程序关闭后清理临时文件?
这些看似复杂的需求,其实都指向一个核心问题:如何在C#中准确检测其他应用程序是否已经关闭。本文将为你提供6种实战级解决方案,从基础到高级,让你轻松应对各种监控场景。
🎯 核心问题分析
在实际开发中,我们经常需要监控其他应用程序的状态,主要痛点包括:
- 时效性要求:需要第一时间感知应用关闭事件
- 资源消耗:频繁轮询会造成性能开销
- 权限限制:某些监控方法需要特殊权限
- 多实例处理:同名应用的多个实例如何区分
针对这些问题,我们需要根据不同场景选择合适的监控策略。
🚀 方法一:Process类基础监控(推荐新手)
最直接的方法是使用.NET内置的System.Diagnostics.Process类:
C#using System.Diagnostics;
namespace AppProcessMonitor
{
internal class Program
{
static void Main(string[] args)
{
// 要监控的应用程序名称(不含.exe扩展名)
string processName = "notepad";
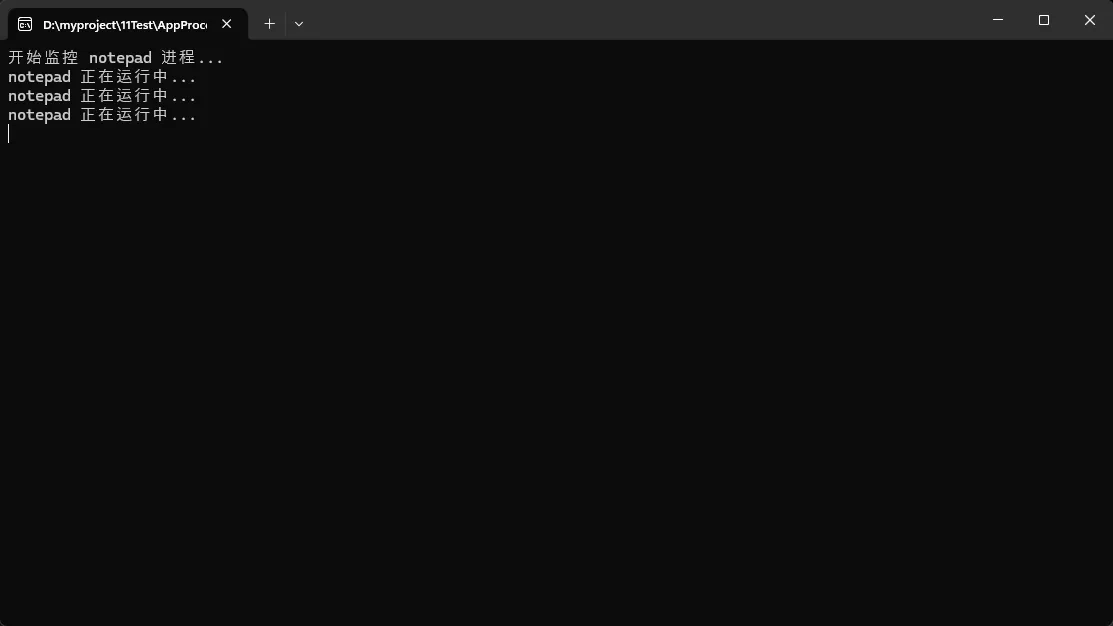
Console.WriteLine($"开始监控 {processName} 进程...");
// 首先检查进程是否正在运行
if (!IsProcessRunning(processName))
{
Console.WriteLine($"{processName} 进程未运行!");
return;
}
// 持续监控进程状态直到关闭
while (IsProcessRunning(processName))
{
Console.WriteLine($"{processName} 正在运行中...");
Thread.Sleep(1000); // 每秒检查一次
}
Console.WriteLine($"🎉 {processName} 已关闭!");
// 在这里执行应用关闭后的操作
}
/// <summary>
/// 检查指定名称的进程是否正在运行
/// </summary>
static bool IsProcessRunning(string processName)
{
Process[] processes = Process.GetProcessesByName(processName);
return processes.Length > 0;
}
}
}
前一篇文章介绍MasterMemory,这个组件讨论的网友挺多了,有网友单独问我,说想用这个替换sqlite,我肯定是不支持的,虽然官方对比sqlite的性能与存储提示不少,但绝对不是db的读取逻辑。所以有了这篇文章,按网友说他现在30w数据在sqlite中大该150M,我模拟写了以下程序,试了一下,30万条设备数据,复杂的多维度筛选,用户输入关键词的瞬间就能看到结果。至于大家用在什么场景还是自己拿主义了。
作为C#开发者,你是否遇到过这些痛点:
- 数据库查询慢如蜗牛,用户体验糟糕
- 复杂的索引设计让人头疼
- 高并发下数据库压力山大
MasterMemory 优点
🚀 性能优势
- 毫秒级查询响应:30万数据查询速度<1ms,比传统数据库快200-500倍
- 零序列化开销:直接操作C#对象,无需序列化/反序列化过程,这个优势还是明显的。
- 预构建索引:启动时一次性构建所有索引,查询时直接使用
- 内存查询:避免磁盘I/O瓶颈,全内存操作
- 基本是source code 预编译的,这个可以看我以住的这个系列,算是写的比较清楚了。
💻 开发优势
- 类型安全:编译时检查,运行时高效,避免SQL语句错误。
- 强类型支持:原生C#对象操作,智能提示完整
- 复合索引支持:支持多字段联合索引,优化复杂查询
- 线程安全:只读特性天然保证线程安全
🔧 技术优势
- 支持复杂查询:范围查询、多条件筛选、模糊搜索等
- 高并发友好:避免数据库连接池压力
- 序列化持久化:支持二进制序列化保存到磁盘
MasterMemory 缺点
📝 功能限制
- 只读特性:数据更新需要重建整个数据库实例,不支持实时增删改,你想用这个替换db需要考虑的东西就多了,要是有时间我可以试试扩展一下它的写。
- 内存占用:30万数据约占用50-100MB内存,大数据集内存压力大
- 数据一致性:更新时需要全量重建,存在数据一致性时间窗口
🔧 技术限制
- 学习成本:需要掌握MessagePack序列化、索引设计等概念
- 过多索引开销:索引数量过多会增加内存占用和构建时间
- 依赖管理:需要额外引入MessagePack等第三方包
💾 存储限制
- 内存依赖:所有数据必须能装入内存
- 持久化复杂:数据持久化需要额外的序列化/反序列化逻辑
- 版本管理:数据结构变更时需要考虑兼容性问题
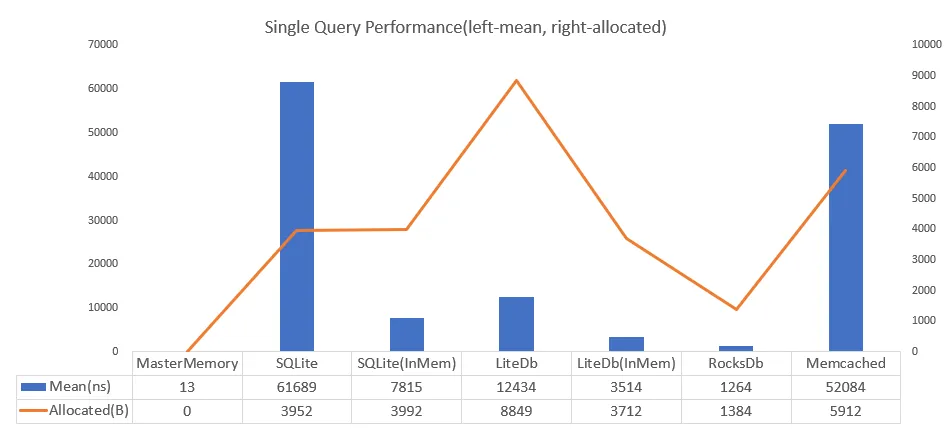
官方性能对比图